GESP编程能力等级认证标四级(复习要点)

GESP编程能力等级认证标四级(复习要点)
Minecraft-Sep2023/12/8 个人笔记
主题:GESP编程能力等级认证标四级(复习要点)
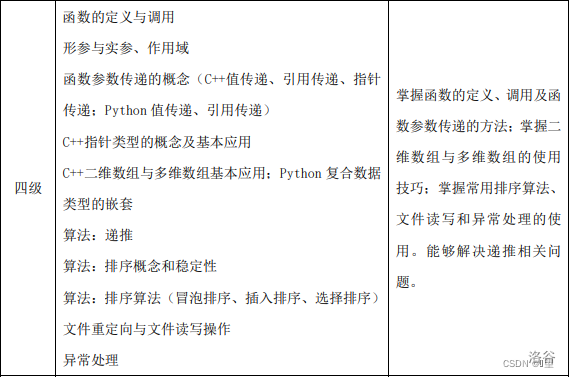
考试大纲
知识点复习
1.形参和实参
定义:
形参:形参出现在函数定义中,在整个函数体内都可以使用,离开该函数则不能使用。
实参:实参出现在主调函数中,进入被调函数后,实参变量也不能使用。
网上很多大佬都是这么讲的,认为举个例子更容易理解:
假设定义了这样一个函数
1 | int f(int x){ |
然后在主函数中这么调用它
1 | int main(){ |
- 那么int f(int x)中的 x x x就是形参(在函数中定义,并只能在此函数中使用的参数)
- 主函数中f(n)的 n n n就是实参(将数据传入函数中的参数)
- 作用域
作用域,顾名思义,就是变量或常量的作用范围(可使用范围)
1 | for(int i = 1; i <= n; i++) |
2.函数的定义和调用
1 | int(返回值类型) f(自定义函数名) (int x(形参列表)){ |
- 返回值类型 :一个函数可以返回一个值的类型
- 函数名:给函数起的自定义名称
- 参数列表:使用该函数时,传入的数据
- 函数体语句:花括号内的代码,函数内需要执行的语句
- return表达式: 和返回值类型挂钩,函数执行完后,返回相应的数据
3.排序的概念和稳定性
| 排序算法 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 冒泡 | $O ( n 2 ) O(n^2) O(n2)$ | $O ( 1 ) O(1) O(1)$ | 稳定 |
| 插入 | $O ( n 2 ) O(n^2) O(n2)$ | $O ( 1 ) O(1) O(1)$ | 稳定 |
| 选择 | $O ( n 2 ) O(n^2) O(n2)$ | $O ( 1 ) O(1) O(1)$ | 不稳定 |
4.文件重定向与文件读写
1 | freopen("a.in","r",stdin)//将输入重定向为从文件a.in读入 |
5. 冒泡、选择、插入排序
一、冒泡
定义
- 冒泡排序(英语:Bubble sort)是一种简单的排序算法。由于在算法的执行过程中,较小的元素像是气泡般慢慢「浮」到数列的顶端,故叫做冒泡排序
过程
它的工作原理是每次检查相邻两个元素,如果前面的元素与后面的元素满足给定的排序条件,就将相邻两个元素交换。当没有相邻的元素需要交换时,排序就完成了。
经过 $i$ 次扫描后,数列的末尾 $i$ 项必然是最大的 $i$ 项,因此冒泡排序最多需要扫描 $n-1$ 遍数组就能完成排序。
性质
1 | // 假设数组的大小是 n + 1,冒泡排序从数组下标 1 开始 |
二、选择
定义
选择排序(英语:Selection sort)是一种简单直观的排序算法。它的工作原理是每次找出第 $i$ 小的元素(也就是 $A_{i..n}$ 中最小的元素),然后将这个元素与数组第 i 个位置上的元素交换。
性质
稳定性 由于 swap(交换两个元素)操作的存在,选择排序是一种不稳定的排序算法。
时间复杂度 选择排序的最优时间复杂度、平均时间复杂度和最坏时间复杂度均为 $O(n^2)$。
代码实现
1 | void selection_sort(int* a, int n) { |
三、插入
定义
插入排序(英语:Insertion sort)是一种简单直观的排序算法。它的工作原理为将待排列元素划分为「已排序」和「未排序」两部分,每次从「未排序的」元素中选择一个插入到「已排序的」元素中的正确位置。
一个与插入排序相同的操作是打扑克牌时,从牌桌上抓一张牌,按牌面大小插到手牌后,再抓下一张牌。
性质
稳定性 插入排序是一种稳定的排序算法。
时间复杂度 插入排序的最优时间复杂度为 $O(n)$,在数列几乎有序时效率很高。插入排序的最坏时间复杂度和平均时间复杂度都为 $O(n^2)$。
代码实现
1 | void insertion_sort(int arr[], int len) { |
折半插入排序
插入排序还可以通过二分算法优化性能,在排序元素数量较多时优化的效果比较明显。
时间复杂度 折半插入排序与直接插入排序的基本思想是一致的,折半插入排序仅对插入排序时间复杂度中的常数进行了优化,所以优化后的时间复杂度仍然不变。
代码
1 | void insertion_sort(int arr[], int len) { |